Chapter 8
My First Experiment
"The
most exciting phrase to hear in science, the one the heralds new
discoveries,
is not 'Eureka!', but 'That's funny'."
Isaac
Asimov (1920-1992)
The Detection of Ether
Even
though in this book the Hafele-Keating experiment was discussed before
my
experiments, which will now be discussed, in reality it was my discovery of
ether
drag in 1998 and 1999 that attracted my attention to the Hafele-Keating
experiment.
As
mentioned in Chapter 1, the debate between ether and photons can be traced
back
to Sir Isaac Newton. Prior to Newton, there were several different theories
about
what light is. After Newton there were only two, and the particle nature of
light
(then called a "corpuscle") was the accepted theory of light. In the
early
1800s,
the corpuscle theory of light was disproven (it failed to correctly predict
refraction).
Also, Young's dual-slit experiment demonstrated that the wave
nature
of light was profound. These two discoveries, and others, combined to
turn
scientific opinion to the wave theory of light - the aether or ether theory of
light.
Then, for a variety of reasons, but mainly because of a second round of
Compton
experiments, the ether theory was dropped in 1924.[22]
Note
that the changes back-and-forth between the wave theory of light and the
particle
theory of light have always included some experiment that indicated the
"wave"
or "particle" nature of light was "stronger"
than believed at the time. The
best
solution to determining what light is, is not to use the
"wave" or "particle"
nature
of light, because light clearly has both properties.
In
November of 1997, I gave a two-hour presentation to the Chief Scientist of the
large
telecommunications corporation where we both worked. I wanted $16,000
to buy
some equipment for Phase 1 of a series of experiments designed to
isolate
why the frequency of fiber optic signals drifted in and out of phase over
time.
I told him that I thought the problem was caused by our earth's total motion
in
space, now known to be 370 kps.
Because
I could not believe that a burst of energy (i.e. an electron quantum drop)
could
be converted into a very complex particle (a photon), as easily as everyone
said
it could, I made it clear to the Chief Scientist that I thought ether probably
62
existed.
For this, and other reasons, I designed Phase 1 of the experiments to
determine
whether ether existed. He carefully listened, but he did not approve
any
funding.
Several
months after my failed attempt to get funding I heard about Roland De
Witte.
Roland had done some experiments in Belgium in 1991 that I had never
heard
of. When Roland sent me a description of his experiments, I forwarded his
email
to the Chief Scientist without additional comment. He understood the
significance
of Roland's discovery.
Roland's
experiments had proven that the earth's motion in space caused a
drifting
in the frequency of electrical signals over time. Roland detected
frequency
changes that had a sinusoidal cycle, with a sidereal day period,
for
178
consecutive days (I will explain all of this in the chapter on the De Witte
experiment)!
Roland's proof that the earth's motion in space affects frequency
changes
is exactly what I had predicted for fiber optic signals. Roland had used
the
pattern of frequency changes to detect a URF, the same URF that is also
called
CMBR, and his experiment roughly estimated our planet's total velocity in
space.
One or two days after I forwarded the email from Roland, I got a call from
a
manager in the Chief Scientist's department asking me how much money I
wanted
for my experiments.
My
approach to detecting ether in Phase 1 had to do with the Big Bang. I felt that
because
ether particles were much lighter than atoms, that the expansion of the
ether
after the Big Bang was significantly faster than the expansion of the visible
universe.
I knew this expansion would slow down over time, and the process of
"thinning
out" the ethons would slow down, but I felt it's expansion was still
faster
than
our very heavy solar system. Because I did not believe in ether drag at that
time,
I had several ideas on how to directly detect the much quicker expansion of
the
ether, all of which involved detecting the bending of light on the surface of
the
earth.
As
part of this effort I built some computer simulations which were composed of a
number
of celestial mechanics formulas, coupled with the direction I intended to
point
my laser continuously over a 24-hour period. For several months we did
experiments,
but we were never able to get the actual experimental results to
agree
with the computer simulations. By plotting where the laser beam hit a
target
over the time period of 24 hours, I was looking for a distorted ellipse
caused
by the bending of light, but I could not get an ellipse, much less a
distorted
ellipse.
See
the graphic on next page for an example of a computer generated nondistorted
"ellipse"
on a target.
63
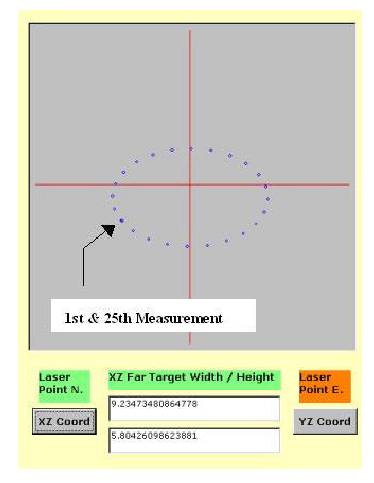
64
Each of
the 25 dots on the target are made by physically marking the target (this
is a
computer simulation), once an hour, and the dot is put where the laser beam
hits
the target. The first and last dots are taken at the same time on consecutive
days
and thus are on top of each other. The width of the above ellipse is
predicted
to be about 9.2 inches (in this hypothetical experiment) and the height
of the
ellipse is predicted to be about 5.8 inches. This hypothetical experiment
was
done at about 39 degrees north latitude with the laser pointed north, thus the
ellipse
is really a circle tilted at 39 degrees.
More
will be said below about why I was expecting an ellipse.
We
kept changing the equipment in order to make our equipment more stable.
Then
one morning at about 6:00 AM, at an experiment site during an experiment,
it hit
me like a bolt of lightning: "I was not going to get an ellipse, when
everything
worked
I was going to get a "dot" (i.e. all 25 points were
going to be on the same
spot),
all of the data we were getting was caused by weaknesses in the stability
of our
equipment!" Over the next 45 minutes I wrote about 10 pages of
notes on
the
ramifications of getting a dot instead of an ellipse. I described an
"Ionospheric
Balloon" of ether and how this Ionospheric Balloon did not rotate
with
the earth, and many other things. I then understood why I wasn't getting any
usable
results from my experiments.
Within
a period of a few seconds I became a believer in "ether drag" (though
I am
not sure
whether I knew of that term at the time), and I knew I was not going to
be
able to detect the expansion of the Big Bang from the earth's surface because
ether
drag was shielding the data I was looking for.
Prior
to this time we had already switched from using a laser to using a telescope
(Note:
This experiment can be done with a laser, but because of beam
divergence,
it is more accurate to use a telescope.), but I realized the telescope I
was
using was not powerful enough to analyze the very small movement of a dot
on a
paper target. We rented a telescope from a science teacher, and on our
first
attempt we got a dot. The movement from the dot on the computer screen
(i.e.
the motion of the point on a piece of paper, from the initial point, recorded
by
our
CCD camera) was random and the maximum movement of the dot was only
5% of
the motion of what the original predicted ellipse would have been.
In a
nutshell, what I discovered is this: "if ether exists, so does ether
drag!"
Since
I already believed in ether, this meant to me that ether drag existed.
However,
even for those who do not believe in ether, it meant that if ether exists,
so
does ether drag. If there were no ether drag, and if ether existed, I would
have
gotten an ellipse due to the motion of our earth towards Leo! The fact
that I
got a
dot is proof that if ether exists, so does ether drag. This might not seem
like a
major discovery, but it eliminates one of the possibilities in the ether-photon
65
debate!
It means that we do not need to consider the possibility that ether exists
without
ether drag.
Because
I was dealing with the "path of light," instead of the
speed of light, and
because
I wasn't dealing with half-silvered mirrors, frequency shifts, or
interference
patterns, there was only one way to interpret my results. This one
discovery
opened the window to experimentally separating the ether theory from
the
photon theory without using the particle or wave nature of light as the
determining
factor. My "null" result (a "dot"
instead of an ellipse) was not really
a null
result at all, I had clearly detected the ether drag if the ether theory of
light
is
true! So had Michelson and Morley in hindsight. Using simple logic, this
means
that we don't need relativity to explain the null result of the
Michelson-Morley
Interferometer experiment.
The Photon Perspective
Thinking
back to the photon theory, aberration of starlight is proof that photons
travel
independent of our earth's motion towards Leo (assuming photons exist).
It
doesn't matter whether the light is from a star, the moon, or from across the
room -
photons are not dragged with the earth. It would be absurd to think that
photons
from distant stars are not dragged with the earth, but photons from
terrestrial
lasers are dragged with the earth.
The
fact that photons move independent of the earth is one of the key reasons
the
ether theory was rejected, because ether drag does drag light with the earth,
but
photons don't. By using the "path of light," meaning the path of a
laser beam
or the
path of light from a target to a telescope, it is possible to
determine
whether
light travels by photons or ether, if we know that if ether exists, so does
ether
drag! This is because there is a vast difference in the path of light
between
the
photon theory (photons are not dragged with the earth) and the ether drag
theory
(in which light is dragged with the earth), using terrestrial light
sources,
which
are entirely inside of the ether drag.
To put
it yet another way, if the photon theory is true, the total aberration of
starlight
(based on our total 370 kps motion towards Leo) could easily be
detected
using terrestrial light because photons are not dragged with the
earth!
But if
the ether/ether drag theory is true, this aberration of terrestrial light will
be
virtually
zero because the light signals will be dragged with the earth! Thus it
is
easy to
make the final determination of whether ether or photons exist -
determine
the aberration of terrestrial light!
Unfortunately,
I have never had access to equipment that could make that
determination
directly, so I have had to jury-rig different kinds of experiments that
ran
into complication after complication. I ultimately had to determine that
terrestrial
light does not have aberration by experimentally detecting
66
phenomenon
that led to paradoxes rather than a direct observation. This actually
had
some unexpected advantages, but it would be nice to directly detect it some
day. I
will now start the process of explaining what I did and why I did it.
Applying the MTLs to My Experiments
In the
case of a terrestrial light source, the platform the target is on is the earth.
For
example, suppose the earth is headed towards a specific spot in the
constellation
Leo at exactly 370 kps. Suppose a laser is aimed exactly
perpendicular
to our vector towards Leo and suppose that a single pulse of the
laser
is fired towards a fixed target 300 meters away.
Both the
laser and the target are attached to the earth, and both are headed
towards
Leo at 370 kps. What happens when the laser is fired, and the laser
beam
exits the laser barrel? To understand what happens, let us think about two
spaceships
traveling side-by-side at 370 kps, 300 meters apart, both headed
towards
Leo. The laser is on one of the spaceships and the target is on the other
spaceship.
Once the laser beam is "in the air," meaning it has left the barrel
of
the
laser and is traveling towards the target, we can instantly ignore the motion
of
the
spaceship the laser is on. Understanding why the spaceship the laser is on
becomes
irrelevant once the laser beam leaves the laser is the whole point of
the
MTLs!
Once the
laser beam is in the air, we focus our attention on the motion of the
target
(i.e. the spaceship the target is on), and ignore the motion of the laser (i.e.
the
spaceship the laser is on). What will happen? The laser beam will miss the
center
of the target because the spaceship has moved at 370 kps towards Leo
while
the laser beam was in the air.
Exactly
the same thing would happen if both the laser and the target were on the
earth.
In other words, it doesn't matter whether the laser and target are on
separate
space ships or whether they are both on the surface of the earth, the
MTLs
apply exactly the same.
The
speed of light is about 300,000 kps. The velocity of the earth is about 370
kps.
Thus, the velocity of the earth is about 0.001233 of the speed of light. So if
the
laser beam travels 300 meters, for example, the target travels about 0.37
meters
towards Leo while the laser beam is "in the air!" This means
the laser
beam
should miss the center of the target where it was originally aimed by about
0.37
meters!
But
now there is a problem, it is impossible to determine exactly where the laser
was
originally aimed because light is also traveling from the target to the laser
(i.e. from
the target to the eyes of the person aiming the laser), and for this light
the
laser (i.e. the eyes of the person aiming the laser) is the moving target. To
67
overcome
this paradoxical problem, it is necessary to build a computer simulation
program
that can, from the spot the laser beam hits the target, calculate where
the
laser was originally aimed. But, by itself, this doesn't prove anything because
it
requires several assumptions. To overcome making any assumptions, the
experiment
needs to be done continually over 24 hours. How this avoids making
assumptions
requires some visualization, which will also help understand the
MTLs.
The Toothpick / Globe Exercise
To
visually understand my experiments, tape a toothpick (pointing north) to a
globe,
say at 40 degrees north latitude. (Warning: Do not use a type of tape that
will
tear the globe's surface.) Also place a string tightly between the center of
the
bottom
of the globe stand and the edge of the table the globe is on (i.e. it must be
straight).
The toothpick represents the vector of the laser beam. The string
represents
the vector of our earth towards Leo.
Now
spin the globe very slowly and note the continuously changing angular
relationship
between the toothpick (i.e. which represents the path of the laser
beam,
the laser is not touched during the experiment) and the string (i.e. which
represents
our earth's path towards Leo). The earth is almost uniformly moving
towards
Leo, but the earth's rotation causes the laser beam (the toothpick) to
change
angles continuously relative to our path towards Leo (the string), which
never
changes during the exercise. Spin the globe several times very slowly. In
the
time the laser beam is in the air, the earth moves along the path of the
string.
The toothpick
is constantly changing angles, but the string never changes its
direction.
Now
lets simulate the actual experiment with the globe. Put a "target" at
the
north
end of the toothpick (the target should be about 5 cm wide). The target, a
small
piece of cardboard, should be normal (i.e. perpendicular) to the toothpick,
and
its center should be touching the toothpick. Attach or tape the target to the
globe.
Now untape the toothpick from the globe. This is because the
laser
beam
will not travel with the earth towards Leo, only the target will move with the
earth.
Hold the toothpick with your fingers and point it to the center of the target.
Put a
mark on the cardboard where the tip of the toothpick is touching the target.
Now
imagine that the laser is fired. Move the globe 2 cm towards Leo (i.e.
towards
the edge of the table along the string). Hold the toothpick in place with
your
fingers and do not move the toothpick as you move the globe. In
other
words,
the toothpick must remain fixed relative to the table while the
globe is
moved.
The 2 cm represents the motion of the earth towards Leo while the
laser
beam is "in the air." Since the target
is taped to the globe, it obviously
moves
with the globe. The motion of the target is significant because the beam
has
not yet hit the target.
68
Note,
do not rotate the globe as you move the globe along the string. The
velocity
of the rotation of the earth is so slow, relative to the speed of light, that
the
earth's rotation is totally irrelevant to this experiment. Any rotation of the
globe
as you move the globe along the string will throw off this demonstration.
Since
the toothpick is not attached to the globe, and you are holding it motionless
in the
air, relative to the table, the toothpick will not move towards Leo with the
globe.
When you have stopped moving the globe 2 cm, the tip of the toothpick
will
not be touching the target at the same place it was touching the target before
the
globe was moved. Now mark the spot where the laser actually hits the
target.
You will now have two marks on the cardboard, the center and one mark
after
moving the globe.
Now
continue to do the experiment for 24 simulated hours by doing the following:
1)
Rotate the globe 15 or 30 degrees without moving it along the string.
2)
Before moving the globe along the string, reset (i.e. realign)
the north tip of the
toothpick
with the center dot on the target (i.e. every time before moving the
globe
along the string, move the toothpick to the original spot on the
target and
at the
original North angle relative to the globe - this is critical), and then
3)
Move the globe exactly the same distance in the direction of the string as
before
(do not move the toothpick with the globe and do not rotate the globe as
you
are moving it along the string), and then
4)
Mark each spot after you move the globe along the string, and then
5)
Repeat the first four steps until you have completed rotating the globe (i.e.
until
you have simulated 24 hours).
You
should see a pattern develop that looks like a very crude ellipse.
Especially
note that half-way through the exercise, after rotating the globe 180
degrees
(i.e. for 12 hypothetical hours of earth's rotation), the new dot is on the
opposite
side of the center of the target than the first dot was. Note also that the
tips
of the toothpick have effectively switched places at this 12 hour mark.
Ponder
these things because they will become very important in the next
chapter.
Each mark
represents what happens if a laser beam is fired at a target. The
target
moves with the earth towards Leo. But aberration of starlight (via the
photon
theory) tells us that the laser beam will not move with the earth towards
Leo.
After the photons are "in the air," the photons will move in a
straight line
relative
to CMBR (the table), and will not be dragged with the earth. Since the
angular
relationship is continually changing between our path towards Leo and
the
path of the laser beam (because of the rotation of the earth), the
"miss" of the
laser
beam will continually change.
69
In
other words, suppose the laser beam were fired 25 times, once an hour, where
the
first and last firing would hit the same spot (well, not exactly, the first and
last
spots
will not be exactly the same spot because the earth is orbiting around the
sun,
but it should be very close). The laser beam would hit the target in 24
different
places. This is because the rotation of the earth constantly changes the
angular
relationship between our vector towards Leo and the vector of the laser
beam.
If fact, if we marked these 24 different positions, they would form an
ellipse
(see the graph earlier in this chapter). The ellipse would actually be a
circle
tilted at 40 degrees (which is the latitude of the laser).
This
is the key: in my experiment I did not need to know where the laser was
originally
pointed. All I needed to do was plot the 25 firings of the laser and the
center
of the ellipse (i.e. the center of the tilted circle) would be where the laser
was
actually aimed during the experiment.
The Actual Experiment
In my
first experiments, I shot a laser at a target 300 feet away (and other
distances
in other experiments). In the time it took the laser beam to hit the
target,
the earth (and thus the target) moved about 4.44 inches (in 3D) towards
Leo
(i.e. 0.37 of one foot). Since the motion of photons (as always, assuming the
photon
theory) and the motion of the earth are independent, I should have
missed
the target by 3.6 inches (in 2D) because of the MTLs.[23]
The reader
might
think that the correct answer would be a 4.44 inch miss, and it would
always
be a 4.44 inch miss in 3D. But remember that the experiment is being
done
at 40 degrees north latitude (actually it was closer to 39 degrees north),
thus
the maximum 2D miss is not equal to the constant 3D miss. Actually, the
3.6
inch number was obtained with a considerable amount of celestial mechanics
formulas
and represents the maximum "miss" (in 2D) over the 24 hours in any
direction
at about 39 degrees north latitude.
In
order to avoid many complications (such as knowing where the laser beam
was
"really" pointing) I did two things. First, I used a computer
simulation and
celestial
mechanics formulas to determine the exact vector of the laser beam to
our
earth's vector towards Leo at any given time. This allowed me to project the
3D
"misses" of 4.44 inches to a projected maximum 3.6 inch
"miss" in 2D.
Second,
and most important, I did the experiment continuously over a 24-hour
period
(one complete rotation of the earth), as already explained.
The
purpose of this experiment was to determine if there is secular aberration of
terrestrial
light with a tilt of aberration of 370 kps. Because photons are not
dragged
with the earth, in the time it takes the laser beam to travel from the laser
(i.e.
think about the photon hitting the center of the top of the telescope) to the
target
(i.e. think about the photon missing the center of the bottom of the
telescope
because of the earth's motion in space), the photons will miss the spot
70
the
laser was actually aimed at. Since we don't know exactly where the laser
was
aimed, we must do the experiment for 24 hours and use the pattern to
determine
where the laser was aimed.
With the
photon theory of light, the markings on the target should have been a
nearly
perfect ellipse, just as if the ether theory were assumed without ether
drag.
With the photon theory, because the photons do not move with the earth
towards
Leo, the full effect of secular aberration should be manifest in the
markings
on the target.
So
what were my experimental results? Once I got my equipment completely
stabilized,
in both laser experiments and telescope experiments, all 25 markings
were
essentially the same spot. In other words, I did not get an ellipse, I got a
single
dot, with very minor noise. This amounts to a null result. This is why I
thought
I had detected ether drag.
Before
going any further, I now need to talk about "path momentum."
Path Momentum:
Now
let us consider another example of the MTLs. Suppose there are two
parallel
train tracks and two trains running "nose-to-nose" at the same
velocity.
Suppose
the archer is on one of the train's flatbed cars and that I am holding a
target
on a flatbed car on the other train. We are directly across from each other.
If the
archer shoots his arrow, and if I do not move the target, it is well known that
the
arrow will hit the center of the target. However, this success is actually the
result
of two offsetting laws.
If the
archer were standing on a stationary platform, and the train the target is on
was
moving to the archer's right, the arrow would hit to the left of
the target due
to the
MTLs. On the other hand, if the archer was on a moving train and the
target
were on a platform, the arrow would hit to the right of the
target due to the
momentum
of the arrow. But in the case we are discussing, both the archer and
the
target are on moving trains, thus the MTLs and momentum offset each other
and
the arrow hits the center of the target (this, of course, assumes no air,
etc.).
I call
the type of momentum that the arrow has: "path momentum," to
emphasize
that the momentum of the arrow affects the path of the arrow.
Relative
to the archer, the arrow does not leave the bow at an angle because the
archer
is moving with the train and he does not see the angle. However, the
archer's
perspective, as always, is irrelevant to the MTLs. The MTLs are
always
concerned
with absolute motion, meaning motion relative to a fixed, unmoving
coordinate
system, meaning the ground in this case. Relative to the ground (i.e.
if we
took a moving picture from a fixed platform high above the trains, the arrow
leaves
the bow at an angle. In other words, the archer thinks the arrow
goes
71
straight,
just where he aimed it. But in fact the arrow leaves the bow at an angle,
relative
to the ground.
Getting
back to my experiment, there is one difference between using terrestrial
light
and star light. With terrestrial light there are variables we have to deal with
concerning
the nature of the light source. In other words, the light leaving the
laser
may have path momentum, which is something that is irrelevant for
starlight.
If photons did not have path momentum, clearly the pattern I got would
have
been an ellipse because photons are not dragged with the motion of the
earth.
Thus, if photons exist, because I got a single dot instead of an
ellipse,
photons must have path momentum.
In other
words, relative to CMBR (which is our coordinate system in all photon
examples),
if photons have path momentum, the photons leave the laser at an
angle. If
they didn't leave at an angle I would not have gotten a dot. We would
not
observe this angle because we are traveling with the earth, just as the archer
above
did not know his arrow left the bow at an angle. Related to path
momentum,
scientists have shown that photons can have a small amount of
mass.[24]
Thus,
what my experiment demonstrated affects both ether and photons. If ether
exists,
my experiment proves that ether drag exists. On the other hand, if
photons
exist, my experiment proves that photons have path momentum.
But
before anyone gets comfortable with photons having path momentum, there
is
another experiment that needs to be discussed in conjunction with my first
experiment.
But first, more preliminary train examples.
Path Momentum and the Photon Theory
In the
just mentioned train example, the arrow was aimed perpendicular to the
direction
of the train the archer was on. We will now discuss what path
momentum
does if the arrow is aimed parallel to the direction of the train.
Now
let us consider another arrow example. Suppose there are two train tracks,
obviously
parallel to each other, going through two parallel tunnels under the
same
bridge or hill. Suppose the two trains are each traveling at 80 kph, but are
going
in opposite directions. Suppose there is an archer on each train
and
suppose
there is a target half-way between the two tunnels, attached to the
outside
wall of the bridge (i.e. the target is fixed and is not moving).
Now
suppose that one train is just getting out of the tunnel and the other train is
about to
enter the tunnel and that both flatbed cars that the archers are on are on
the
same side of the tunnel, the side that the target is on, but their respective
trains
are traveling in opposite directions.
72
Now
suppose that at the exact instant that both archers are across from each
other
(meaning they are exactly the same distance from the target), they both
shoot
an arrow at the target with exactly the same bow energy.
Here
is the question: will both arrows arrive at the target at the same instant of
time
and with the same velocity? The obvious answer is "no." The arrow
shot
from
the train heading into the tunnel will have significantly greater velocity than
the
arrow shot from the train heading out of the tunnel.
This
difference in velocity is caused by exactly the same "path momentum"
as
discussed
above when the two trains were traveling in the same direction. The
only
difference is that these arrows are shot parallel to the direction of the
trains -
one
forward and one to the rear.
In
exactly the same way that path momentum applies to arrows, my experiment
proves
that path momentum applies to photons. If arrows or photons have
perpendicular
path momentum, they also have parallel path momentum.
My
first experiment proves that photons have path momentum when the laser is
shot
perpendicular (or nearly perpendicular) to the direction the earth is headed.
It
would therefore be ludicrous to assume that photons do not also have path
momentum
when the laser or light source is pointed in a parallel direction to the
path
of the earth towards Leo.
In a
real archer example, the velocity of the arrow is affected by the velocity of
the
train the archer is standing on. In other words, the motion of the train the
archer
is on actually causes the velocity of the arrow to increase.
This is
general
physics. Because the arrow leaves the bow at an angle, it must travel
further
to the target than if both trains were standing still. Thus, even though the
arrow
has to travel further if both trains are in motion (think of the diagonal of a
right
triangle), the increased speed of the arrow caused by the motion of the train
the
archer is on (i.e. path momentum increases the speed of the arrow) offsets
the
increased distance of following the diagonal.
Because
I got a dot (instead of an ellipse), it is clear that the photons traveled
along
the diagonal of the triangle. However, because I got a dot (instead of a
smaller
ellipse) there is evidence the photons increased their velocity due to the
motion
of the earth towards Leo. In other words, if the photons had traveled
along
the hypotenuse or diagonal, but did not increase their velocity due to the
motion
of the earth, I still would have gotten an ellipse, but it would have been
much
smaller than the original ellipse.
This
is all very nice theory, but in fact my equipment was not accurate enough to
guarantee
that the velocity of the photons (assuming the photon theory) did
73
increase.
Therefore, I must rest my case on the general physics of momentum -
momentum
does increase the velocity of objects.
Thus
using general physics, if we shot laser beams, instead of arrows, at the
target
attached to the tunnel wall, and if the trains were traveling at 370 kps (and
the earth
were stationary in the universe), the velocity of the photons hitting the
target
would be the speed of light, plus or minus 95% of 370 kps (I use 95%
because
my most accurate experiment, which used a telescope, was only 95%
accurate).
This means that the speed of light would be c-v and c+v (adjusted by
no
less than 95% of v, where v is the velocity of the earth towards Leo). Again,
all of
this is discussion is assuming the photon theory. With the ether theory
things
are totally different.
The First Major Paradox in This Book
There
are only two ways to explain why I got a dot:
1)
Ether exists and there is ether drag surrounding the earth (note that the
experiment
was done completely inside of our ether drag, thus the laser, the
target,
and the light beams would all be dragged together with the ether drag and
a dot
would be predicted), or
2)
Photons have path momentum and the speed of photons is c-v and c+v,
where
v is the velocity of the earth.
But
now there is a problem with the photon theory. Based on the c-v and c+v
which
would result from the path momentum of photons, it is absolutely clear that
the
Michelson-Morley Interferometer ("MMI") should not
have received the null
result.
In other words, my null result proves c-v and c+v, but that is exactly what
Michelson
and Morley were looking for! The MMI could have detected
differences
in the speed of light well below 30 kps (remember back then they
were
assuming our total velocity in space was only 30 kps), but my experiment
proves
that the speed of light varies by at least plus or minus 351 kps if
the
photon
theory is true! In other words, the velocity of light must be 300,000
kps
plus
or minus 95% of 370 kps, meaning 300,000 kps plus or minus 351 kps, if the
photon
theory is true. The MMI, and numerous interferometers build since then,
could
easily have detected such a vast difference in the speed of light.
The
MMI experiment (and many other interferometers), which deal with the
speed
of light (which are looking for c-v and c+v), and
my experiments, which
deal
with the path of light (which prove c-v and c+v),
meaning the MTLs, could
not
both have gotten null results if the photon theory were true. If photons have
path
momentum, then the MMI should not have gotten a null result. But if
photons
do not have path momentum, then my experiment should not have
gotten
a null result.
74
But
both experiments could have gotten null results with the ether drag theory
because
both the speed of light and the path of light are relatively constant within
the
ether drag (the speed of light would only be affected by our earth's rotation
speed).
There
are other experiments that need to be mentioned. The Sagnac effect
proves
that the velocity of light on the surface of the earth is c-v and c+v, but in
this
case v is not the total velocity of our earth through space, but
it is the
rotation
velocity of the earth at the latitude of the
experiment. In other words,
the
Sagnac effect, the Michelson-Gale and Pearson experiment, discussed in
Chapter
1, and the Hafele-Keating experiment, also discussed in Chapter 1, have
all
detected the ether wind being equal to the rotation velocity of the earth! This
should
be a clear signal that ether and ether drag exist. Now we will move on to
my
second experiment.
75