Chapter 6

Chapter 6

The Moving Target Laws

"A ship in port is safe, but that's not what ships are built for."

Grace Hopper. (The computer term "bug" is also due to Grace Hopper)

Introduction to The Moving Target Laws

When I talk about the "path of light," I am really talking about the Moving Target

Laws. It is critical for the reader to have an exact understanding of what the

Moving Target Laws are in order to understand any of my experiments or the

Lunar Laser Ranging experiments. This chapter will provide that understanding.

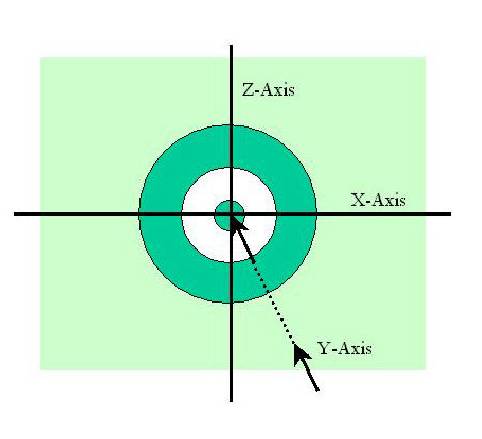
Consider an archer who is a perfect shot and always hits the exact center of the

bulls-eye. Now consider the archer and his target as a three-dimensional

coordinate system. The two-dimensional target is on the X-Z plane. The path of

the arrow is the Y axis. The X axis, Y axis and Z axis all meet at a point that is

also the center of the bulls-eye of the target. Suppose further that the archer is

100 feet from the target.

See graphics on next page.

Now suppose the archer aims at the target and that I am holding the target.

Suppose that after the arrow leaves the bow, but before the arrow gets to the

target, two things happen: 1) I move the target one-foot straight up and 2) the

archer throws the bow into a trashcan. The arrow will obviously land one foot

below the (center of the) bulls-eye. This example, as with all examples, assumes

the archer is a perfect shot, there is no arch on the arrow, the experiment is done

in a vacuum, etc.

The key to understanding the Moving Target Laws (MTLs) is to understand the

slice of time between:

1) The instant after the arrow leaves the bow and

2) The instant before the arrow hits the target.

This slice of time is the time the arrow is "in the air." "In the air" means the

arrow is no longer attached to the bow, and has not yet hit the target. While the

arrow is "in the air," what happens to the archer and the bow is irrelevant

because the arrow is no longer attached to the bow. As I implied above, while

the arrow is in the air, the archer can throw the bow into the trashcan and this act

will have absolutely no affect on where the arrow hits the target. While the arrow

is "in the air" the bow and arrow are totally independent of each other.

But the same cannot be said about the target. While the arrow is in the air, it is

headed towards the target. Thus any motion of the target, while the arrow is in

the air, has a direct affect on where the arrow hits the target! This is why they

are called the "moving target" laws.

The MTLs basically study the motion of the target during the slice of time the

arrow is in the air. In the example just given, after the arrow leaves the bow, but

before it gets to the target, the target is moved one-foot straight up. Thus the

moving of the target has a direct affect on where the arrow hits the target.

More Examples of the MTL

If I were to move the target exactly one foot down while the arrow is in the air, the

arrow would land one foot above the (center of the) bulls-eye. If I move the

target exactly one foot to my right (while the arrow is in the air), which is to the

archer's left, the arrow would miss the target by exactly one foot to my left. I am

behind the target so the arrow would hit to the left of the bulls-eye from my

perspective. But from the archer's perspective, the arrow would land to the

archer's right (i.e. the archer would see the arrow land one foot to the right of the

bulls-eye). And so on.

Now let us do thousands of these exercises. Suppose that after the arrow leaves

the bow, that I am allowed to move the target exactly one foot on the twodimensional

X-Z plane, and that I can move the target in any of the 360 degrees

of the plane. If we were to do this exercise thousands of times there would be up

to 360 holes that would form a perfect circle (i.e. the holes would all be on the

outside edge or perimeter of the circle), with the center of the bulls-eye being the

center of the circle. No holes would be inside or outside of the perimeter of

holes.

Now let us construct an imaginary three-dimensional sphere with the center of

the sphere being the center of the bulls-eye. The imaginary sphere has a radius

of exactly one-foot. Now let us change the rules. I can move the target exactly

one foot while the arrow is in the air, but I can move it in any direction in threedimensions, as long as the center of the target ends up being on the surface of

the imaginary three-dimensional sphere when the arrow arrives.

In other words, the center of the bulls-eye will always be on the surface of the

imaginary sphere by the time the arrow arrives. Since the sphere is in three

dimensions, but the target is only in two dimensions, I can move the target such

that the arrow can hit any point within a one-foot radius of the center of the bullseye.

As an example, if I were to move the target along the Y-Axis, directly towards the

archer or directly away from the archer, ignoring the arch of the arrow, the arrow

would hit the center of the bulls-eye even though I moved the target one-foot. If I

were to move the target slightly off of the Y-Axis, the arrow would just miss the

bulls-eye.

Now suppose this three-dimensional experiment were done thousands of times

and I moved the target randomly. In this case an imaginary circle of one-foot

radius on the target, with the bulls-eye at the center, would have many arrow

holes in it or on its perimeter. In other words, instead of just being on the

perimeter of the circle, the holes would also occupy the inside of the circle.

Now suppose we studied one specific hole in the target. Let us suppose that I

moved the target one-foot at such an angle on the sphere that the arrow missed

the center of the target by exactly 5 inches. Studying the angle that the hole is

from the bulls-eye, the angle that I moved the target could easily be determined.

However, since the target itself has only two-dimensions, it could not be

determined whether I moved the target generally towards the archer or generally

away from the archer (on the Y-Axis). Thus the solution to exactly how I moved

the target in three-dimensions could only be reduced to two possibilities.

If an observer were standing on the side of the target, she could note whether the

target were moved forward or backwards because she would see the Y-Z axis.

Thus she could determine the Y-Axis movement and narrow the possibilities

down to one.

More Complex Archer Examples

Now let us suppose that I am standing on a flatbed car on a moving train. Again,

I am holding the target. We will assume the archer is standing on a train station

platform. The flatbed car is moving with the train (along with the target), but the

archer is not moving. Let the distance between the archer and the target be 100

feet.

Let us assume that the train is moving at such a speed that in the time it takes

the arrow to travel to the target the train moves exactly 1 foot (the train is in

constant motion). Now suppose the archer lets go of the arrow at the exact

instant that the bulls-eye passes him. Now suppose that I do not move the

target, but hold it still. The arrow will again miss the target by 1 foot. If the train

is moving left to right (per the archer), the arrow will land to the left of the bullseye

by 1 foot.

If additionally I had moved the target one-foot in the direction the train is

traveling, the arrow would miss the bulls-eye by 2 feet. It would miss the bullseye

by 1 foot because of my moving the target and another foot because of the

moving train.

However, if I moved the target in the opposite direction the train is traveling, the

arrow would hit the center of the bulls-eye. The 1-foot miss caused by the

motion of the train would be offset by the 1-foot miss caused by my moving the

target.

In these cases the platform that the target is standing on (i.e. the flatbed car) is

in motion, thus the motion of the platform has a direct affect on the motion of the

target while the arrow is in the air. The MTLs apply both to my movement of the

target, and to the platform's movement of the target. Anything that moves the

target while the arrow is in the air is significant to where the arrow hits the target.

In the experiments that are discussed in future chapters, the platform will be the

earth, the archer will be a laser, and the arrow will be a laser beam.

One of the hardest things for people to grasp about the moving target laws is that

once the arrow or laser beam is "in the air," the motion of the archer or the

motion of the laser is irrelevant. People constantly wonder why the motion of the

archer or laser is irrelevant. Many examples will be given to make this distinction

clear.

The MTLs will be mentioned many times in this book. They are not only the

basis of aberration of starlight, but are also directly involved with all of my

experiments and any experiment that involves the path of light.