TUTORIAL NOTE 12
Welcome to the Second 'Semester' of Ten Tutorial Notes, which
teach the mathematical basis of Aether Science theory.
INERTIA AND ITS IMPLICATIONS
© Harold Aspden, 1999
Here we will enter into the formal
analysis of one of the most basic features of physics, the relationship between
inertia and instantaneous action-at-a-distance.
Take an electric charge
e, assume that it is accelerated under the influence of other electric charge
and examine the physics of what happens. I ask you to accept as your starting
point two hypotheses: (i) that the electric charge will not under any
circumstances radiate any of its energy and (ii) that its electrical action at a
distance, meaning its electrostatic field external to its body of charge, will
only experience change as effects which propagate at infinite speed, that is
virtually instantaneously.
If you have any formal training in physics,
beyond high school standard that is, then you will know that both of these
hypotheses are quite unacceptable to the orthodox professionally qualified
physicist. I am therefore asking you to follow an argument of heresy just to see
where it leads. You will be surprised at the result.
To ease your concern about what has just been suggested I refer to
a remark which J S Bell, a recognized authority on quantum theory, made in
speaking to a distinguished audience on the subject of action-at-a-distance in
quantum mechanics. He said that Lorentz invariance has "become very
problematic" and that "an ether would be the cheapest solution". [See the text
of his lecture at p. 269 of v. 10 of Speculations in Science and Technology
(1987)].
The unitary charge e is that we assign to the electron,
but it could apply to any particle comprising such a unitary charge, whether of
positive or negative polarity.
If we depict that charge in a figure, what
will you draw? Will it be a point or perhaps a sphere or, as was once suggested
to me by a Professor of Physics, a vector diagram denoting something called
'spin'?
Before we get into the detail of that, it is appropriate to
summarize some background information, that of my background. As a university
student back in 1946 I invested in the purchase of an academic textbook entitled
Modern Physics. It was by H A Wilson, the Wilson involved in the
'Schuster-Wilson Hypothesis' (see LECTURE NO. 4). Professor
Wilson had academic qualifications from Leeds, Cambridge and London Universities
in England but was Professor of Physics at Rice Institute in Houston, Texas at
the time he wrote that book. He was also a Former Fellow of Trinity College,
Cambridge, the venue of Isaac Newton and the physicist who discovered the
electron, J J Thomson.
So, as my funds were scarce, when I say I
'invested' in that book, I meant it. I expected it to be of benefit to
me.
Now at the time, being 18 years of age, I was not the least bit
interested in Einstein's theory, but I was interested in electricity. That book
meant a great deal to me when I made my way forward on the electrical front. It
clarified the physics which in turn helped me in my more practical study of
electrical technology. I may note here that the book had, indeed has, 432 pages,
but, although entitled Modern Physics it was not until page 245 that
there was any reference to Einstein's Theory of Relativity and that was a terse
statement: "According to Einstein, energy has mass, and the mass of energy E is
equal to E/c2, where c is the velocity of light." One then had to
turn to page 345 before encountering a discussion of the Michelson-Morley
experiment and "the idea adopted by Einstein as the basis of his theory of
relativity." A little further on the book took aboard the full thrust of
Einstein's Special and General Theories of Relativity, giving a detailed account
of the tensor theory involved and working systematically through the
complications of the General Theory to show how, for example, the anomalous
perihelion motion of planet Mercury was explained in its full detail.
I
read all that and understood it, but it was of no immediate interest and it
certainly had no utility so far as my career interests in electrical technology
were concerned. However, in later years I came to realise that Einstein's theory
had blocked the scope for initiatives aimed at advancing the technology that
depended upon knowledge concerning the way in which the aether stores energy. In
other words Einstein's theory was obstructing technological advance.
Of
course, you will say that E = Mc2 was a triumphal achievement
dependent upon Einstein's theory and its role in the field of atomic energy
contradicts the statement I have just made. However, if you say that, then you
need to know a little of what was described in the early pages of Professor
Wilson's book. It was on page 8 that Wilson discussed Poynting's theorem and by
page 9 he had covered electromagnetic momentum, which led, by page 10 to a
formulation of energy E as having a mass that is effectively E/c2.
Still on page 10, and with no hint that Einstein had any hand in the work of
building such a theory, we see how easy it is to derive a formula which says
that energy and so mass escalates to infinite value as the object having that
energy and mass approaches the speed of light. On page 10 we see what would
later be referred to by physicists as Einstein's 'relativistic mass equation',
but yet there has been no reference to Einstein or his methods in deriving that
formula.
The reason, in simple terms, is that the facts of electron
theory, of energy and the increase of energy and mass with speed were known from
experiments performed in the late 19th century and before Einstein appeared on
the scene.
This brings me then to page 15 in Wilson's book, where he
reproduces a method devised by J J Thomson for explaining the Larmor radiation
formula for the energy radiated by an accelerated electric charge. I shall in
this Tutorial Note be working through the analysis involved, but I want you to
know what Wilson stated on page 16 as he ended that analysis. It reads:
"Electromagnetic radiation is obtained in practice from electrical
oscillations produced by the discharge of a condenser through a wire. In such
cases, in which enormous numbers of electrons are involved the radiation
obtained agrees with that calculated by electromagnetic theory. Radiation from
single electrons has not been observed, and according to the Quantum Theory
the electrons in atoms do not radiate when they are moving around orbits and
so have an acceleration. The success of quantum theory makes it possible that
the expression just obtained for the radiation of an electron is erroneous,
and in fact that the equations of the electron theory are probably only true
when the density of electricity us taken to be the average density over a
large volume containing a large number of electrons and atomic
nuclei."
So you see, here, by page 15 in a 432 page textbook
directed at the serious student of physics as a precursor to research
specialization in a particular field, Professor Wilson has revealed something
that is surely extremely important and warrants very careful consideration. Why
is it that the analysis by that J J Thomson method works for electricity in
bulk, but not for the isolated electron? Surely physicists cannot hide behind
the magic principles of Quantum Theory! Yet that is exactly what the full might
of the academic physics establishment has done for most of this 20th century.
They have ignored that problem which was assuredly presented in the 1937 edition
of Professor Wilson's book, if not expressly stated in his first, 1928,
edition.
Now when I came to focus on this particular problem, which I
certainly did once I had my own Ph.D. as a qualification, I saw so clearly that
the J J Thomson derivation of the energy radiated by the accelerated electron
had not taken any account of the necessary electrical field producing that
acceleration. It had just been assumed that somehow the electron was accelerated
as if the statement "Let there be acceleration" was akin to God's biblical
utterance: "Let there be light". Accordingly I set about incorporating the field
that produces the acceleration to see how that affects the analysis. I had,
incidentally, by the time I embarked on this task in 1954, convinced myself that
there is an aether, a real aether, so I was beginning to rebel against the
influence of Einstein's theory and was ready to challenge virtually anything
that lacked true substance and a ring of truth.
We will first see the
derivation of the radiation formula assuming no accelerating field is active and
then correct the analysis by rectifying the assumptions involved.
The J J Thomson Method
We will use the cgs system of units to simplify
presentation.
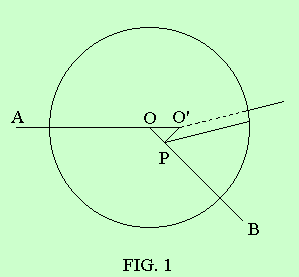
Referring to Figure 1,
consider an electron moving along a straight line AO with constant velocity v.
At and near to O suppose the velocity changes abruptly to a constant velocity v'
along OB. While the electron is moving along AO its electric field moves with
it. At O where v changes it will begin to excite the electric field
corresponding to velocity v' along OB, and at the time interval t later this new
electric field will fill a sphere of radius ct. Here c is the assumed speed at
which the change of field propagates radially from that point O. Outside the
sphere the field will still be that due to the electron moving with velocity v
along AO. The two fields will be separated by a layer of thickness c.dt
containing the field excited by the electron during the short interval dt in
which its velocity changed from v to v'. The layer moves out with the velocity c
and it contains the wave produced by the change from v to v'.
The lines
of force in the field outside the sphere of radius ct will radiate from the
point O' on an extension of the line AO, where OO' is vt and the lines of force
inside the sphere radiate from a point P on OB such that OP is v't. If we
consider a line of force starting from P and making an angle θ with O'P, it will
be displaced relatively to the parallel line outside the sphere by a distance
(O'P)sinθ, and we may suppose these two lines are joined into a single line by a
part lying in the layer of thickness c.dt. This requires a field component in
the layer, in the plane containing O'P and parallel to the surface of the
sphere, equal to:
(e/r2)(O'Psinθ)/c.dtwhere r = ct, because the radial
component in the layer is equal to e/r2. When t is zero the line of
force considered is all outside the sphere of radius c.dt, and as t increases
the relative displacement (O'P)sinθ increases proportionally to t. Thus a line
inside the sphere corresponds to a parallel line outside.
At this stage
we can introduce an acceleration term denoted (v'')/dt. This is the rate of
acceleration f of the electron, v'' being the vector difference betrween v' and
v. Note that O'P is (v'')t, so that the tangential field in the layer under
consideration is:
efsinθ/rc2Note that by 'tangential' field is meant
the field component directed at right angles to the direct radial field lines
emanating from O.
The electric energy density in the wave region defined
by that tangential field component in that field layer is 1/8π times the square
of this field component and, based on Maxwell's theory, we suppose that there is
an equal amount of magnetic field energy, so we can formulate the energy in the
whole wave as:
 This is the energy radiated
in time dt while the velocity of the electron changed from v to v' and so the
rate of radiation of energy is:
This is the energy radiated
in time dt while the velocity of the electron changed from v to v' and so the
rate of radiation of energy is:
2e2f2/3c3
This brings us to
the formal classical derivation of the rate of energy radiation by an electron
owing to its acceleration. However, we are going to question this result,
because somehow electrons can be accelerated in an ongoing everlasting life
within their abode inside an atom and there is no energy radiated unless the
atom is excited by some quite dramatic external influence so as to drive the
electron to an energy level by which it is forced into an unstable
state.
Experiment says that electrons suffering the enormous rates of
acceleration they experience within atoms do not radiate energy in a continuous
emission process such as that implied by the above analysis.
Now, there
are several points that we can make at this stage. Firstly, if the electric
field could adjust to the electron's change of velocity instantaneously, as if c
were infinite, then there would be no energy radiation and the problem would
disappear. Secondly, there is an implicit assumption in the analysis based on c
being finite, which is that the electric field can adjust instantaneously to the
electron's change of position (as opposed to velocity). How else can we justify
the assumption that the field lines all move bodily as a unit sharing the
velocity of the electron? They ought otherwise to bend, the faster the electron,
meaning that they should be distorted as a function of speed even though that
speed is constant. So this second point actually obliges us to adopt the
argument that c is infinite so far as the electrical action is concerned and
that means no energy radiation.
Our third point arises if we now ask how
the electron can be accelerated. Presumably the electric field interaction of
another charge or group of charges in the environment of the electron is at work
promoting that acceleration. That field must have a field intensity F which is
equal to mf/e, where m is here the mass of the electron. This field acts in the
direction of acceleration but will not affect the energy radiated except for its
component in a direction common with that of the above-mentioned tangential
field. In fact it will have such a component Fsinθ that is negative, because the
tangential field lines emanating from the charge are stepped backwards in
relation to the forward acceleration field direction.
Now, in the above
calculation, we have squared the electric field intensity and we have not taken
account of this field F. Let us do that. You will then find that there is a
condition for which the resulting electric field energy density in the radiated
wave is zero. In working this out we must only consider the components of energy
density that amount to a wave disturbance, because we cannot suppose that any of
the normal energy of that field F is radiated. The relevant factor in the energy
calculation is:
[ef/rc2 - mf/e]2subject to our exclusion
of (mf/e)2. This gives a factor proportional to:
(ef/rc) - 2mf/eand this tells us the condition for which there
is no radiation of energy for c finite.
The condition is that:
e2/2r = mc2
Now we have argued that
there really can be no continuous radiation of energy by that discrete charge
when accelerated, as we well know from quantum theory, so we know that this
equation has to be valid. Yet if we put c as infinite to cater for that
instantaneous action which assures that no energy is radiated through regions
well remote from the sphere of influence of the accelerating field F, then that
energy expression mc2 becomes infinite. To make sense of this we need
to say that the charge e is a point charge, so that r is zero and that just
cannot be. I well know that quantum physicists like to think that the electron
is a point charge, but it does have a finite mass and so a finite rest-mass
energy.
What, therefore, the above equation does tell us is that the
electron has a finite form, a spherical form containing the charge e, but that
the finite speed c applies within that charge sphere, whereas the propagation
speed outside the body of charge becomes infinite. We can then interpret the
equation in the following way. Note that if we denote the radius of the electron
charge as a, it says that where r is equal to a at that charge
boundary the energy quantity e2/2a, now denoted E, is equal to
mc2, always provided the electron conserves its energy to avoid loss
by radiation.
In other words E = mc2 for the very reason that
the desire of that electron not to shed that energy by radiation, its desire to
conserve its energy, has caused it to react to that applied field F in just such
a way that it acquires the property we have come to know as 'inertia'.
Furthermore the measure of its inertial mass is determined by its intrinsic
electric energy E by a derived formula which says that mass is equal to E
divided by the square of propagation speed of disturbances set up within the
body of charge.
So the situation you now confront is an electron that
tells you that E= Mc2 without there being any appeal to Einstein's
theory, a theory which, incidentally does not explain the nature of inertia, but
merely declares the equivalence of inertial mass and gravitational
mass.
You will no doubt have many questions to raise in your effort to
cast doubt upon my conclusion here, so I will raise some of those questions
myself.
Firstly, where is that electric energy located. It amounts in
fact to the electric field energy disposed outside that radius a. What
does this mean? It means that the task confronting that field F is to accelerate
the mass of the electron as seated outside its body of charge. So now you put
the question as to whether there is electric field energy inside that body of
charge. The answer to this is affirmative, because the energy density inside the
charge, where c is the uniform finite speed of disturbance propagation, is
itself uniformly distributed and, to avoid discontinuity at a is equal to
that at a, meaning that it is 1/8π times
(e/a2)2. Multiply this by the volume of the
electron charge sphere and you will find that the extra energy of the electron
attributable to this is:
(1/6)(e2/a)which makes the total mass-energy
of the electron equal to:
(2/3)(e2/a)precisely the value derived by J J
Thomson by an alternative method involving magnetic field theory!
Your
next question then could be: "What about the wave radiation conveying energy
through the body of that charge? How does that affect the above
calculation?"
The answer to this is that it has all been worked out and
is of published record on pages 82 and 83 of my book Physics Unified
(1980). The added mass of the electric field being accelerated adjusts exactly
to satisfy the condition that no energy is radiated and the energy/mass formula
of the electron applies to that Thomson energy value. The analysis is simple and
straightforward. Test your mathematical skills and see if you can verify that
yourself.
So now we have understood that the electron and, indeed, any
discrete particle of unitary charge will exhibit the property of inertia and a
mass equal to E/c2 and will not radiate energy. The next question to
raise is the perplexing issue of c being constant and finite within a body of
electric charge. Does c really have the same value within such charge forms of
different physical size? How can it be that c is infinite in empty space, space
devoid of those discrete forms of charge e, and yet finite inside the body of
such charge? What have I to say about magnetic fields and the fact that
electromagnetic waves travel at the finite speed of light c through space devoid
of matter?
Let me remind you of that comment by J S Bell. He was
concerned with action-at-a-distance in quantum theory and felt that the answer,
the 'cheapest solution' in the expenditure of scientific brainpower, was to
revert to a belief in the aether.
We have introduced action-at-a-distance
in saying that c could be infinite where c is the speed at which electric field
action propagates in free space, meaning in space between discrete electric
charge forms. So now we must face that question concerning magnetic
fields.
First, however, we need to dispose of the minor question
concerning c being the same in charges of different size. Here I can but appeal
to an analogy with the known properties of gas. Compress a given quantity of gas
into spheres of different size. The pressure will increase inversely as the
volume decreases and the mass density will increase with the pressure, but the
square of the speed of propagation of sound in those gases is proportional to
the pressure divided by the density. It is the same whatever the volume taken up
by that standard amount of gas. I do not see this as proof for the corresponding
case of the electric charge, but it is suggestive that there could be some
common factors governing the physical circumstances involved. Certainly, if the
argument is restricted to conserved mass and energy, and volume is varied,
energy density divided by mass density is independent of volume and we can infer
from the physics of dimensional analysis that the speed parameter is independent
of volume.
The question of magnetic field raises with it the question of
what happens when groups of electrons are accelerated in unison. This is the
situation in a radio antenna and we do know that energy is radiated, or rather
shed, by such an antenna, radiation being a questionable term because it implies
that the energy shed actually travels at the speed of light and there is nothing
to confirm that that is the case. The answer to our magnetic field problem is
found in the fundamental roots of the physics of electrodynamics.
Now
already I have introduced you to this subject in Tutorial No. 3. If you
seek further enlightenment then I refer you to my published paper 'Instantaneous
Electrodynamic Potential with Retarded Energy Transfer' [1988a]. You
need to work out the Neumann Potential starting from the Coulomb electric
interaction as being an instantaneous interaction, but involving two electric
charges that are in motion relative to one another. Once you have derived the
Neumann Potential you can deduce the law of electrodynamics and from that you
can go on to derive the familiar theory of the magnetic field.
That step
of going from the Neumann Potential to the law of electrodynamics involves
recognition of a role played by the aether, meaning charges in the aether
reacting to disturbance.
So, ignoring now that electrical field F
introduced in the above analysis, suppose, because we have two charges that are
interacting, that you work out the energy radiation formula at a distance well
removed from the source and replace e by 2e. You will get the propagating field
energy density as being proportional to (2e)2 and wonder if one can
deduct the twice the single e component or 2e2 to get a net radiation
of energy in the Coulomb electrostatic field gauge. For a million such charges e
oscillating together the difference escalates to make that standard Larmor rate
of energy radiation derived by the J J Thomson method seem acceptable. However,
that infinite value of c for the action-at-a-distance in that Coulomb gauge is
still effective in reducing the net rate of energy radiation to zero. Much as we
have tended in the past to accept the Larmor radiation formula when adapted to
the multiple charge oscillation, we must come to terms with that zero-radiation
result and accept the inevitable conclusion that it does not apply to the
acceleration of an isolated electron.
It means that electromagnetic waves
are set up by the oscillation of electric current and its effect in setting up
magnetic fields which disturb the aether and, being 'magnetic', they represent
energy in transit from a photon source to a region of photon absorption, energy
which is pooled with the energy sea of the aether. Yes, those oscillations of
aether energy imply aether charge displacement and waves which are local
oscillations as between electric displacement energy and kinetic (magnetic)
energy. The action complies with Maxwell's theory but only if that theory is
modified to put the electric and magnetic field oscillations into quadrature
time phase, meaning that as one rises to its maximum the other falls to its zero
state. That way, the energy is conserved and does not travel at the finite speed
c, which is the wave velocity.
The standard teaching concerning
electromagnetic waves requires you to believe that the electric and magnetic
fields, though in space quadrature, meaning one oscillates from right to left as
the other oscillates up and down, both reaching their maxima and minima
together. That forces energy dissipation. It is a feature governing the
operation of most radio antennae, but, though its effect is to shed energy quite
effectively, it is not the best way of exciting electromagnetic waves that have
to travel long distances. I can but refer here to the Gieskieng antenna
experiments, the subject of the Appendix to Lecture No.
10 in these web pages.
Note that if you discharge a capacitor through
a straight wire the surge of current will develop an induced back-EMF as the
energy is absorbed into the magnetic field, where it is stored. However, the
current involved surges through the resistance of the wire causing some loss
and, further, because that current is not in time-phase quadrature with the EMF
applied by that capacitor it forces a condition in which the aether finds itself
at odds with itself because it wants to sustain a natural oscillation as between
the electric and magnetic disturbance. Accordingly it takes on board energy
which it then finds a way of rejecting as heat adding to its entropy. There is a
phase angle between the antenna EMF and the current and this is dealt with in
theory by asserting that it accounts for radiation resistance, the theoretical
assumption being that all the energy injected into the oscillations of those
electromagnetic waves is carried away at the speed of light.
All this
means that we have theory which scientists are happy with, theory which says
that electromagnetic waves radiate energy but yet that requires photons to
convey that energy, theory which denies action-at-a-distance, but yet conflicts
with what experimental evidence concerning quantum theory tells us by implying
what amounts to superluminal speed of communication. So my argument is that if
one really looks deeply into the case put by H A Wilson concerning the radiation
of energy by the accelerated electron, one can see scope for correcting errors
implanted in that theory. I suggest that there is no such thing as energy
radiation at the speed of light, given that what travels at the speed of light,
if tangible in energy terms, must have infinite mass, so posing an impossible
scenario. I suggest instead that waves, as travelling disturbances of energy
already in the aether, will involve the forward and backward low speed
displacement of aether energy, while the wave itself, meaning the surface
envelope of that aether energy travels at that high but finite speed c.
I
further suggest that, whereas in that J J Thomson method of deriving the Larmor
energy radiation formula, Wilson added magnetic field energy in amounts equal to
the electric field energy, basing his argument on the assumption that electric
field energy is forcibly propagated and that it develops Maxwell-type waves, the
fact is that current oscillations in an antenna set up a propagating magnetic
wave oscillation which deploys aether energy, as from a standing reserve of
energy in the space through which the wave travels, but into a compliant local
electrical field oscillation in time-phase quadrature.
The aether is
essential and action-at-a-distance in the Coulomb gauge is equally essential.
The consequences technologically could be that we have already been missing
opportunities in exploiting new types of antenna for radio communication, if not
opportunities to tap energy from the sea of aether energy that is omnipresent. I
note that the latter was deemed feasible long ago by Tesla, but will not enlarge
on that theme. I see the Gieskieng research as warranting scrutiny and have
stated my case on that in that above-referenced Appendix to Lecture No.
10.
There will be many who happen to read this Tutorial Note who will
stand ready to defend what they have been taught about radio communication. They
know that an antenna has a radiation resistance and see the calculation of that
resistance in their textbooks. They are well aware that so much is already known
about radio communication that it seems foolhardy to suggest that there is a
startling gap in that spectrum of knowledge. However, all they really know for
certain is that they inject energy into an antenna to excite its current
oscillations and that somehow the signals generated are detected by radio
antennae elsewhere. The electromagnetic waves are real and they suffer
attenuation with distance travelled much as is expected from the theory taught
in those textbooks, though when physicists get into the act and start talking
about photons carrying the energy then the picture gets a little hazy. So where
have things gone wrong?
The answer is found in an analogy with message
communication using a homing pigeon. You can send messages from A to B by
writing notes and having them carried by the homing pigeon. There are two ways
of doing this. You can put the pigeon in a cage and ship the cage by regular
transport so as to convey that pigeon with its message from A to B or you can
release the pigeon at A and give it an initial 'nudge' to let it fly free and
naturally in finding its way by flying from from A to B. The situation with
radio waves is only slightly different. Our forebears designed a transit route
which effectively puts your message in what I will term a 'Maxwell cage' and
forces the transportation of that cage from A to B. Their research caused them
to misinterpret that initial 'nudge' as being something that had to be sustained
during the whole transmission from A to B.
Nature has a natural way of
conveying those messages, but the scientist seeks to force his will on that
process by insisting that the 'cage' travels as well. It is just a question of
whether the energy needed to initiate the wave has to travel at the speed of the
wave or whether it cannot keep up and so is dispersed in the early stages of the
journey.
Clerk Maxwell introduced us to displacement currents and devised
what my Cambridge University Professor, E. B. Moullin, described as 'Maxwell's
Hypothesis', namely the notion that electric currents can only flow in closed
circuits and those displacement currents in the aether duly keep faith with that
requirement.
Once an electromagnetic wave is well clear of its
transmitting source it relies solely on those displacement currents as we know
from the four equations defining Maxwell's proposition:
(K/c)dE/dt = curl H
-(μ/c)dH/dt = curl E
div E = 0
div B =
0
The significance of the symbols used in these equations is well
known so I shall not define each such term. These equations literally 'force'
the message to convey energy with it at the speed of light, but that is mere
'hypothesis'. Had the equations been formulated in a symmetrical form, symmetry
being a theme blessed by many a physicist, then they would have the form:
-j(K/c)dE/dt = curl H
-j(μ/c)dH/dt = curl E
div E = 0
div B =
0where j is a familiar symbol signifying a quadrature phase shift or,
in a mathematical sense, the square root of minus one, it being a turn through
90o, so as to be a vector reversal when squared. If I say this second
set of equations represents 'Aspden's hypothesis', and use this instead of the
Maxwell version, then I will still get those electromagnetic waves propagating
from A to B at the speed of light. They will convey no energy from A to B but
they will convey that message, thanks to the auspices of the aether ruffled by
those waves. That initial 'nudge' is a price paid in powering the conventional
antenna in forcing an in-phase initial condition of the electric and magnetic
field vectors when their natural 'free-flight' aptitude is to fall into phase
quadrature.
Remember here that the whole concept of of magnetic field H
is only notional. H is something invented to provide a link between two systems
that convey electric charge and so involve currents acting on currents. The -1
connection that applies to real currents in the real inductive circuits of the
matter form is no warranty that the displacement current at a point in free
space has to partner another current to define that -1 term. Physically, if what
is meant by E2 and H2 as energy quantities can be energy
drawn from the matter state, when we talk about actions in circuits on our
laboratory bench, but energy borrowed from the aether when we are well into free
space, then E2 plus H2 might apply to the matter state and
E2 minus H2 might apply to the free space aether proper.
That two-step j phase shift converting +1 into -1 really does need to be
considered seriously.
So if you adhere to the conventional philosophy
concerning radio waves then you are probably living in a state of ignorance, not
knowing how energy really travels at the speed of light or what happens to that
energy when waves crash into each other as they move in opposite directions. You
are not destined then to research the problem of how two such waves crashing
into each other sustain their frequency characteristic as they emerge, nor will
you be able to discover how a very sparse population of pseudo-matter, Nature's
ongoing attempts to shed energy in free space to create protons and electrons,
will progressively reduce the wave frequency as a function of distance
travelled. So you will not then see how this explains the cosmical phenomenon
called the 'redshift' and you will be destined to think that the universe is
expanding from a point in the seat of a lengendary 'Big Bang'. In short, bearing
in mind that very nearly everything we know about outer space depends upon the
interpretation of the physics of electromagnetic radio waves, your defective
knowledge on that subject has aided and abetted in the distortion of the true
physical picture of our universe.
Take note, if you are an old 'student',
that this is all because you were misled into thinking that an accelerated
electron radiates its energy! If you are a young student then take heart and
learn more from these Tutorial Notes so that you can help me in my ongoing quest
to discover the truths of these issues. Remember, some physicists are still
struggling to solve a problem they have with the electron, namely the 'fact', as
they see it, that the electron appears to have mass but no volume. They say that
more money is needed to build bigger and better particle accelerators so that
they can solve such problems, but I suggest that reading a few old textbooks,
such as that by H. A. Wilson, reading them in a questioning way, might provide
answers that can ease much of that pressure to justify more and more research
expenditure.
My primary object in this Tutorial No. 12 has been to
introduce you to the fact that E=Mc2 is a consequence of energy
conservation by electric charge in avoiding radiation of energy and the further
fact that its inertia as such is the phenomenon that it exhibits in that effort
of conservation.
I urge you not to be impressed by Einstein's theory,
simply because you think that the physics of E=Mc2 proves Einstein
right. Theoretical physics has no future if those involved cannot wake up and
focus on the inconsistencies prevalent in their orthodox interpretation of
photons, electrons, the wave versus particle in radiation, and such like.
Technological development is held back so long as this state of affairs
persists. It is necessary to rethink some of the basic problems, not forgetting
action-at-a-distance, and I hope this Tutorial No. 12 will help in that regard
but I will say more on this theme in Tutorial no. 18.
To progress to the next Tutorial press:
Tutorial No.
13
*


