Now I shall call such particles 'gravitons' and declare that the graviton family includes the 'super heavy electron', otherwise known as the tau or taon. In fact, it was discovered experimentally long after I developed this graviton theory. Indeed, there was a period when I thought there was only one form of graviton, a particle which was about 45% more massive than the taon or nearly three times the mass of the proton.
Next, I must introduce a particle form which does not play a direct role in the gravitational action but does dominate the whole stage. This particle form provides the energy that keeps the action alive. It is hidden centre-stage. This is the 'heavy electron', a part of the ghost world of the aether, the 'virtual muon'. Muons have a mass between 206 and 207 times the electron mass, whereas the taon has a mass some 3485 times that of the electron. Physicists will tell you that quantum electrodynamics as applied the field activity in the vacuum medium is made alive with electrons, muons and taons and their anti-particles appearing in pairs as if from nowhere and then disappearing again, but they will not tell you how all this accounts for gravity. Indeed, they do not know because they have not bothered to learn about what I am revealing to the world in these tutorial notes. They have not bothered to study my earlier writings and I can say that because, if they had, they would have been endorsing what I say and writing about this gravitational theory for many years by now.
There are, therefore, muons and taons active in that underworld we call space, but which I call the aether. We will need to deduce the masses of these particle forms in terms of the mass of the electron and we will also need to look for even more massive and less massive particle forms that sit on either side of this taon-muon-electron mass spectrum. The path to G will not be easy, but, if we really can check progress by deducing the relative masses of these particles as we proceed and the results fit well with experimental observation, then we know we are on track in our quest.
To complete the aether particle picture I will now declare that my research told me there are three other aether particle forms, which I will call the 'supergraviton', the 'graviton' and the 'quon', respectively. They all have the same unitary charge magnitude as the electron. That charge quantity is denoted e. However, the quon has a mass much smaller than that of the electron, and the supergraviton has a mass much larger than that of the graviton or the taon.
So far as our derivation of G is concerned, I shall, in this initial stage of analysis concentrate my attention on the standard 'graviton' form. The reason is that I came to realize, as the theory developed, that gravitational forces are seated in particles of the graviton family that work together like wolves in a pack. There has to be at least one standard 'graviton' in a particle cluster that mediates in setting up the force of gravity. It acts as a buffer for minor energy fluctuations.
Accordingly, the first step in deducing the link between G and e/me, the charge to mass ratio of the electron involves the assumption that there is a perturbation in which the standard 'graviton' sheds energy which becomes the matter mass form that corresponds to the forces attributable, as gravity, to the corresponding change of state of that graviton.
To proceed, you need to picture all elements of matter as sharing a common synchronized motion, all those elements moving in tiny circular orbits about an inertial frame. Then the gravitons must be pictured as moving in counterbalance in orbits of the same radius, so that, denoting the radius r, the separation distance between the matter frame and the graviton frame becomes 2r. Then, sitting in the inertial frame and defining that frame are the virtual muons and these have no orderly motion, being subject to a kind of random activity and contributing nothing to that orbital motion which is the basis on which we shall account for gravitation.
You may now be wondering how there can be an orderly circular motion of particles forming a kind of crystal structure but yet able to dissolve and allow counterflow of those particles as part of that Fresnel aether drag scenario presented in Tutorial No. 5. Accordingly, I present below a figure copied from p. 39 of my 1975 book 'Gravitation'. S denotes the forward velocity of the whole system of the aether charges (denoted q) and you can see that some are in free counter-motion in jumping backwards to balance overall momentum. This is only a notional picture. Indeed, these charges q could well merge to become part of the muon background and migrate backwards through the lattice as muons. This does not affect our analysis leading to the derivation of G.
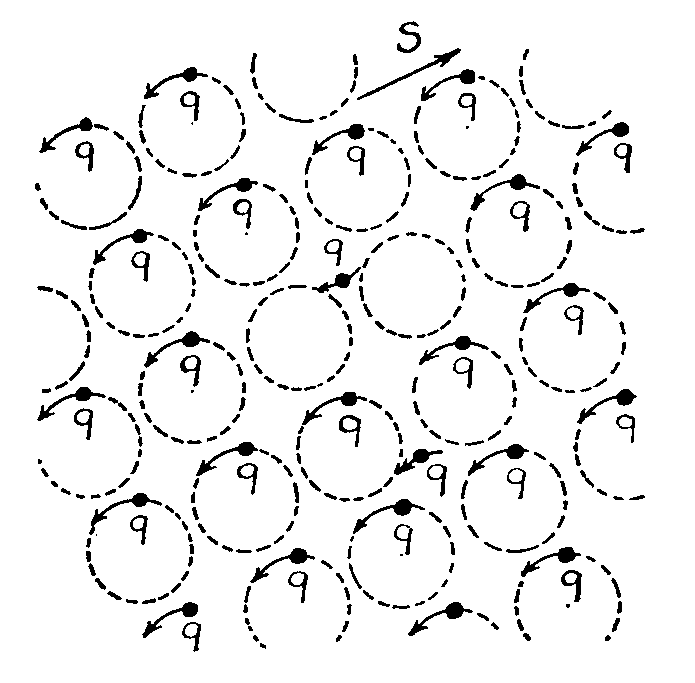
The relative velocity of the graviton frame (the G-frame) and the matter frame or electromagnetic frame (the E-frame) will be assumed to be c, this being a natural speed parameter we surely recognize as a property of the vacuum medium. Therefore, any electric charge that happens to be part of that G-frame will interact electrodynamically with other such charge, but will not interact electrodynamically with matter charge at rest in the E-frame. Furthermore, that speed c will make the electrodynamic effect of a charge e in the G-frame seem to have the strength we associate with electrostatic interactions and so, even though gravitation is an electrodynamic force, we will not see c in our eventual formula linking G and e/me.
The task now becomes more simple. We need to look for a change of the volume of space occupied by a graviton charge and resulting from the perturbation in which that graviton sheds energy. Then, provided the graviton is immersed in a background continuum that has itself a uniform charge density, we can relate that change in volume with a quantity of electrical charge to which we can attribute the gravitational effect. If we know the mass-energy of the graviton, we can work out how it changes volume dV as it sheds energy. If we know the charge density of the background continuum σ we can then formulate a value for G.
You do not need to be a genius then to see that:
Now write the mass-energy of the graviton as Eg and relate this to
the particle radius g by the J.J. Thomson formula:
You should have arrived at the equation:
We shall need to move on to the next tutorial session before we can evaluate oo and I am therefore going to anticipate the result here so that we can develop the formula for G further. We shall see that the aether comprises cubic cells of side dimension d and in each such cell there is a quon (denoted q in the above figure) of charge e balanced by an equal amount of charge of negative polarity dispersed uniformly as that continuum charge σ. That σ quantity becomes e/d3.
The result I shall prove later is the fact that d/a is 108π, where a is the
radius of the electron according to the J.J. Thomson formula by which:
It follows then that the graviton/electron mass ratio Mg/me is equal to a/g, the inverse of the radii of these charges.
We can now combine the relationships presented above to derive the formula:
The Role of the Taon
The standard 'graviton' which features in the above formula for G serves a role in shedding or absorbing energy in interacting with the creation and annihilation of gravitating energy in the electromagnetic reference frame in which matter is seated. The process is a conservative process in energy terms, meaning that the energy fluctuations can occur as perturbations rather than quantum events associated with the creation and demise of particles and their anti-particles. The latter activity, so far as the graviton side of the action is concerned, is where the taons play their role.
Note that the standard graviton will itself exhibit a gravitational effect commensurate with its overall charge volume. You can easily verify that the energy to volume ratio of the whole graviton is one third that applicable to a perturbation where a small increase in charge radius accounts for the gravitational action of the energy shed by that increase in radius. This is where we need to introduce quantum gravity and the taons. The taons have a larger charge volume to energy ratio and so can partner the graviton so that, overall, the charge volume to energy ratio is the same as for the perturbation of the graviton. Note that there will be two taons, one of each charge polarity, and they can exchange energy by one expanding slightly and the other contracting, conserving their combined volumes but with very little energy shed externally. So we shall regard the cluster of one graviton and two taons as a unit, the overall charge volume of which is, in relation to overall energy, precisely equal to that dV/dEg ratio which applied to graviton perturbation.
Formulated, this results in the following equation involving x, the ratio of
the masses of taon and graviton, Mt and Mg, respectively:
We can let the graviton mass be unity along with its volume and energy for
our immediate task in deriving the above equation, whereas the mass or energy of
the taon becomes x and its volume 1/x3. The combined volume to energy
ratio of two taons plus one graviton is then the ratio 1+2/x3 to 1+2x
and this ratio has to equal 3, which is the corresponding factor for the
graviton perturbation. From this you obtain the equation:
You can easily verify that x is then slightly greater than 0.6884, which
means that, once we can know the actual masses of the graviton or taon, we can
evaluate G. The taon is the super-heavy electron of the lepton family and its
mass-energy is known from experiment. So you could look that up in data tables
and check how we are progressing in our quest to solve the mystery of
gravitation by deriving the value of G. However, that was not how I came to
solve the mystery and I would rather guide you along the route I followed in my
research.
The Search for Evidence of the Graviton
This means going back in time to a period before scientists had discovered the taon and so we shall follow the few clues afforded by early particle physics such as were based on cosmic ray analysis. Of course, having obtained a formula for G in terms of graviton mass, I did work out the value of mass, or rather mass energy, needed by that graviton. It bore no resemblance to any particle of matter, being about 5063 times the mass of the electron or, in mass-energy terms, 2.587 GeV. I developed my aether theory in the 1950s and wrote my first printed publication on the subject towards the end of 1959, so it is appropriate to quote from a Table entitled 'Properties of Known Sub nuclear particles (1959)' that I see in a book I now have in my possession. The book is entitled 'The Nature of Physics' and its author is Peter J. Brancazio. It was published in 1975 by Macmillan Publishing Co., Inc of New York.
The list comprises baryons, mesons, leptons and massless bosons and gives
masses in electron units and MeV, but the following data are in electron units.
The baryons are the Ξ- of 2586, Ξo of 2573, the negative,
neutral and positive Σ particles of 2343, 2338 and 2,338, respectively, the Λ
neutral particle of 2183 and two nucleons, the neutron of 1839 and the proton of
1836 electron mass units. The mesons are the neutral kaons of 974, the charged
kaons of 966, the charged pions of 273 and the neutral pion of 264. The leptons
are the negative muon of 207, the electron of 1 unit mass and also listed are
the the muon-neutrino and electron-neutrino of zero mass. Finally, the massless
bosons are the photon and the graviton.
Yes, there is a 'graviton'
mentioned as having zero mass! It is said to be 'stable' and to have a spin of
2, whereas the photon has a spin of 1, but it is merely a name for a
hypothetical particle that mediates in the gravitational force.
So we
have textbook authority dating from a 1959 listing that says our graviton has no
mass. How then did I manage to proceed in seeing a connection between those
baryons and mesons and my graviton? Well, let me say that my original data
source, a 1952 book by R E Marshak entitled Meson Physics, gave slightly
different numbers for some of the particles and even gave the charged pion mass
as 276, which is too high, but this helped, rather than hindered my efforts at
the time. I had enough to piece together some evidence that pointed to that
graviton form at a mass of about 5063 electron mass units. The easiest way for
me to report on that here is to quote a section of text from pages 112 to 114 of
my book 'Physics Unified'.
I had just presented the analysis
showing how a basic energy quantum of 412.665816 electron mass units could be
derived by my theory and followed this by:
"This happens to be very close to the energy of two muons, which are heavy electrons with a mass between 206 and 207 times that of the electron. Accordingly, it is tempting to suggest that the unit cell of the space medium comprises a pair of virtual muons in general migration and providing the equilibrium for the energy of the lattice particle."
[Note that this lattice particle is the 'quon' referenced earlier in this Tutorial.]
In recent times heavy particle decay has come to be characterized by the emission of dimuons. Indeed the ratio of hadrons to dimuon pairs produced in high energy collisions has become an important parameter in particle physics.
It occurred to me that one way in which to discover the mass of the graviton would be to suppose that it was a heavy particle which could decay by producing energy quanta Eo corresponding to a muon pair plus the quanta 1843 electron rest-mass energy units, with the residual energy forming hadrons. [Note that this 1843 quantity had also emerged from the theory and we shall be deriving that in Tutorial No. 8 in this series.] Thus, in a book published in 1966, my book 'The Theory of Gravitation', 2nd Ed., I proposed that gravitons of energy g might decay into pairs of muons plus pairs of the 1843-quanta plus one or two hadrons. Apart from single graviton decay a double graviton decay suggested by collision seemed possible. The need to separate the hadron energy from the 1843-quanta suggests that the latter escape in pairs to assure momentum conservation. Below a tabulation is given of the energy needed to create 1 or 2 muon pairs and 0, 1 or 2 1843-quantum pairs. The former require 412 electron energy units and the latter 3686. An exclusion rule was applied by which the number of muon pairs could not exceed the 1843-quantum pairs by more than one. This excludes the combination 2, 0 as well as 3, 1 and 4, 1 etc.
The following Table summarizes the data that appeared on pages 81 and and 82 of that 1966 book. The data is also tabulated at page 119 of my book Physics without Einstein, published in 1969.
| Hadron Energy Product of Graviton Decay | ||||||
|---|---|---|---|---|---|---|
| No. of particles | Energy in electron units | |||||
| gravitons | muons | 1843 | leptons (L) | gravitons (G) | hadrons (G-L) | |
| 1 | 2 | 0 | 412+0 | 5064 | 2(2326) | |
| 1 | 2 | 2 | 412+3686 | 5064 | 966 | |
| 1 | 4 | 2 | 824+3686 | 5062 | 2(276) | |
| 2 | 2 | 2 | 412+7372 | 2(5063) | 2342 | |
| 2 | 4 | 4 | 824+7372 | 2(5064) | 2(966) | |
Bearing in mind that we contemplate a decay of either one or two gravitons, the table tells us that the energy g is likely to exceed 4510, the combined energy of two pairs of muons and a pair of the 1843 quanta (see the third listed decay), with the fourth and fifth listed decays involving 2g. The first decay would then leave a hadron energy greater than 4098. This seemed too high from 1966 data to correspond to a single hadron. Accordingly, a pair of hadrons was deemed to be formed of energy (g-412)/2. The second decay suggested that the hadron product would be a meson of much smaller mass. There were two candidates, the pion or the kaon. A fit was found by using the kaon of energy value 966 (this is a positive kaon of today of 493.7 MeV). There was a sigma hyperon of mass 2326 (1189 MeV) amongst the few well-known hadrons of the early 1960 period. When a pair of these were put into the first decay, the same g value emerged. Next, the fourth listed decay from two gravitons gave another mass value of the sigma hyperon family 2342 (1197 MeV).
The author, therefore, felt that the pattern emerging gave evidence of the graviton in the region of 5063 electron mass units (2.587 GeV). This was particularly encouraging because this is the value which gives us the constant of gravitation, G.
I have, incidentally, listed the 1843 energy quantum under the lepton heading, even though it is not of itself a lepton. The reason for this is that I wanted to group it with the muon energy to signify that it represented energy absorbed directly into the aether medium or released from that medium by leptonic activity, rather than being surplus energy that could manifest itself in hadronic matter form. My other justification is that this 1843 quantity is derived in my theory as being the number of electrons and positrons (which are leptons) that can be formed within the volume of space taken up by the quon. Indeed, it was this notion that put me on course for deducing the precise value of the proton-electron mass ratio, as being due to the periodic happenings when a number of muons come into existence inside a quon charge owing to the ongoing the quantum electrodynamic fluctuations of the aether.
Now, recapitulating, I can say that I derived the formula for G in terms of a graviton mass in the early 1960s period, having fully developed the basic model for the structured aether in the latter part of the 1950s. The onward search to establish evidence for the mass value of the graviton led to the above picture of decay processes linked to baryons and mesons. Note that, of the lepton family, the electron and the muon featured in the theory, but the taon had not appeared on the scene and the neutrino was not deemed anything other than a manifestation of an aether event in which momentum was transferred. It did not warrant comment, because it was invented to explain something that needed an aether reaction, but, with the aether outlawed, the neutrino concept had to stand in, as it were, even though it is meaningless as a particle form.
The onward development of the theory of gravitation, as already reported in the author's 1966 book 'The Theory of Gravitation', 2nd. Ed., included the formal derivation of graviton mass by pure theory, but the presentation of that must await our analysis of the aether model and the derivation of the heavy electron mass, that of the muon. Thereafter, we will turn attention to the proton and then come back to show how the taon mass comes about. In this way, by a double-pronged attack on the graviton problem, we converge on its creation from two directions and it is a feature of the author's theory that if physical processes occur and, by coincidence, form similar energy quanta that are quasi-stable, then particles having such energy will appear in a dominant manner. The graviton is such a particle, albeit one belonging to that 'ghost' world providing dynamic balance for real matter, but it exists alongside the virtual taon in filling the gravitational role.
The constant of gravitation, G, is only one of the several major advances you will learn about as you now proceed with this sequence of Tutorials, but our next task is to engage in the primary analytical problem now confronting us, namely the determination of the governing parameters of the structured aether.
To progress to the next Tutorial press: