PŘESUN HMOTY

'Úvod'

Založený na experimantální práci na

University of Sussex

Prof. E.R. Laithwaite a W.R.C. Dawson

SYSTÉM PRO PŘESUN HMOTY ODVOZENÝ OD
PRINCIPU ZACHOVÁNÍ MOMENTU

Většina systémů pohonů, které se dnes používají, spoléhá buď na uplatňování síly proti povrchu, nad nímž se pohybují (např. auta, vlaky, lanovky), nebo urychlují materiál, který tvoří médium, v němž se pohybují, ve směru opačném k pohybu, jímž se pohybují (například vrtulová letadla, lodě s lodním šroubem nebo lodě poháněné vesly), nebo využívají tepelně nebo gravitačně odvozeného gradientu energie (například plachetnice), nebo vypuzují materiál ve formě paliva, které je uloženo ve vozidle, jako je tomu částečně v případě tryskového motoru nebo úplně u raketového motoru. Jestliže se vozidlo pohybuje v prostoru, kde není významně přítomno médium, s nímž může reagovat, potom není jiná alternativa než požití naposled jmenované metody.

Když porovnáme výkon dosažitelný pomocí tryskového motoru, kde velká část materiálu vypouštěného z vozidla není nesena na palubě, ale je odebírána z atmosféry před vozidlem, raketový motor je velmi neúčinný. Energie, která přímo nepřispívá k pohonu vozidla, je ztracena přeměnou v teplo, zatímco obrovské množství těkavého paliva, které je třeba nést na palubě, představuje nebezpečí jak pro loď, tak pro posádku nebo náklad. Dolet a ovladatelnost vozidla jsou značně omezeny množstvím paliva v nádržích a jakmile je loď urychlena, zpomalení může být dosaženo jedině spotřebou dalšího paliva.

Práci, kterou jsme udělali na University of Sussex s gyroskopy, nebo – v obecném smyslu - se setrvačníky, umožňuje, aby hmota byla přemisťována lineárně bez reakce s okolním médiem, nebo éterem a bez vypouštění hmoty z vozidla. Kde existuje médium, tj. na zemi, na moři nebo ve vzduchu, stupeň generování momentu se zdá být nezajímavý. Avšak za absence média, v kosmickém prostoru, mimo snadnou dostupnost a tam, kde je požadována zvýšená manévrovací schopnost, je použití tohoto systému nejen výhodné, ale přímo jedinečné. Poprvé nabízí prostředky k udělení lineárního pohybu dodáním malých „kousků“ okamžitého momentu vozidlu ne nepodobné současnému způsobu, pomocí něhož se kosmické lodě přesměrovávají aplikací principu zachování úhlového momentu. Nyní můžeme nabídnout zařízení, které umožní vozidlu, řečeno metaforicky, „plavat vesmírem“.

VYSVĚTLUJÍCÍ ÚVOD K PŘESUNU HMOTY

POHYB OBJEKTU BEZ JEHO STRKÁNÍ

Když chceme pohnout předmětem, který se jeví být vzhledem k nám v klidu, je naší běžnou zkušeností, že je nutné použít sílu, abychom to provedli. Je to proto, že ten předmět má hmotnost, která mu dává vlastnost, jíž se říká setrvačnost. Setrvačnost má tu vlastnost, že brání tělesu v tom, aby získalo rychlost (nebo ji ztratilo – pp). Vztah mezi těmito vlastnostmi byl poznán Newtonem a obvykle se píše (síla) = (hmotnost) x (zrychlení).

Newton vlastně tvrdil: „Síla je přímo úměrná rychlosti změny momentu.“

A co je to vlastně moment, proč se s ním máme zabývat?

Základní zákon, týkající se energie, je, že nemůže být vytvořena ani zničena.

Odněkud přišla a někde musí být nějak absorbována. Nikdy se neztratí. Může tato podmínka, sama o sobě, umožnit nám vyřešit všechny naše problémy v mechanice?

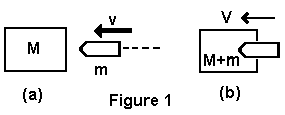
Uvažujme problém kulky vystřelené do nehybného dřevěného hranolu, jak je naznačeno na obrázku 1.

a) Kulka o hmotnosti m je vystřelena rychlostí v do dřevěného hranolu o hmotnosti M

b) Kulka se zavrtá do dřeva a oba se pohybují rychlostí V.

Jak vypočítáme rychlost V?

Stačí nám položit rovnítko mezi kinetickou energií před nárazem a po nárazu, protože energie nemůže být zničena, a vyřešíme rovnici pro neznámou proměnnou V.

A když rychlost V změříme prakticky, zjistíme, že je nižší než byl teoretický předpoklad. Proč? Odpověď je, že část kinetické energie se spotřebovala na zavrtání se kulky do dřeva, přičemž se vyvinulo teplo a zvuk. Kolik energie se takto převedlo, nemůžeme říci!

Newton tento problém vyřešil. Energie má mnoho podob a může být přeměněna z jedné formy na jinou. Existuje jako potenciál, jako teplo, světlo, zvuk, elektřina a magnetismus, stejně jako kinetická energie. Newton vlastně řekl, „Když místo energie zachováte moment, dostanete správnou odpověď, protože moment není převoditelný na jinou formu energie.

Nyní položením rovnítka mezi moment před a po nárazu,

mv = (M + m)V

a vyřešením této rovnice pro V, dostaneme správnou odpověď. (Ovšem při zanedbání přeměny části kinetické energie na teplo a zvuk – pp.)

ROZBĚH A ZASTAVENÍ

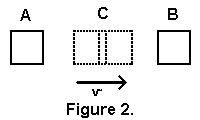
Podívejme se nyní na obr. 2. Těleso se pohybuje z bodu a do bodu B. Jestliže jsou body A a B na stejném potenciálu, není teoreticky potřeba žádná energie pro pohyb mezi těmito dvěma body. Avšak aby se těleso mohlo pohybovat, musí během přesunu do bodu C získat rychlost. Proto z bodu A do bodu C musí být těleso urychlováno. K tomu je potřebná síla. Jestliže na těleso na určité dráze působí síla, je tím vykonávána práce, to znamená, je vynakládána energie.

Předpokládejme, že těleso o hmotnosti m získá maximální rychlost v uprostřed dráhy v bodě C. Vykonaná práce se projeví jako kinetická energie mv²/2. Nyní musí být těleso zpomalováno, aby se v bodě B zastavilo. K tomu je také potřeba síla – síla opačného směru. Teoreticky by se energie, potřebná k zastavení, tělesa měla rovnat energii k jeho urychlení (tj. kinetické energii tělesa v bodě C).

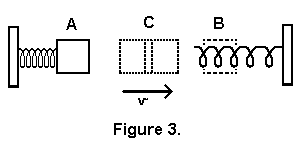
Uvažujme například, že počátečního urychlení by mohlo být dosaženo pomocí pružiny, jak je nakresleno na obr. 3. Energie uložená v pružině jako potenciální energie je přeměněna na kinetickou energii mv²/2. V bodě B bude k zastavení tělesa opět použito pružiny, pomocí níž se kinetická energie promění zpět na potenciální energii.

Jestliže bod ukotvení pružiny by nyní mohl být přemístěn do bodu C, bylo by možné použít ji k posunu hmoty ještě dál doprava, atd. Této metody by nemohlo být použito k pohybu ve volném prostoru, protože pružina musí mít ukotven jeden konec, proti němuž by mohla působit; ve volném prostoru však není žádný kotvicí bod, o který by se jeden konec pružiny mohl opřít.

AKCE A REAKCE

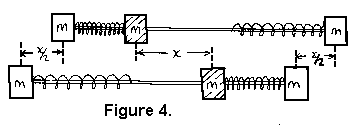
Obrázek 4 ukazuje dvě tělesa, obě mají hmotnost m, spojené lehkou tyčí. Další těleso, také o hmotnosti m, se může po tyči pohybovat. Levá pružina je použita k pohonu tělesa z bodu A do bodu B. V bodě B se těleso zastaví působením další pružiny, přičemž ztratí svou kinetickou energii, kterou získalo díky levé pružině. Jak se celá soustava bude pohybovat?

Označme urychlující sílu pružiny jako F. Počáteční zrychlení pohyblivého tělesa je F/m. Zbývající dvě tělesa, spojená tyčí, budou mít zrychlení o hodnotě F/2m opačného směru. Na konci urychlování , tj. uprostřed tyče v bodě C, se pohyblivé těleso posunulo o vzdálenost x, zatímco spojené hmoty se pohnuly o vzdálenost x/2 opačným směrem.

Můžete vidět, že těžiště se vůbec nepohnulo: hmotnost m se pohnula o vzdálenost x jedním směrem a hmotnost 2m se pohnula o vzdálenost x/2 opačným směrem.

To samé platí pro jakoukoli jinou polohu. Je zřejmé, že jsme absolutně neschopni přemístit cokoli, co je absolutně uzavřené v krabici. Pouze vyhozením materiálu mimo krabici do prostoru (jako raketa) můžeme krabicí pohnout.

PŘÍMOČARÝ A KRUHOVÝ POHYB

Přímočarý pohyb zahrnuje následující veličiny:

Přímočaré přemístění (vzdálenost)

Přímočará rychlost (míra změny vzdálenosti s časem)

Přímočaré zrychlení (míra změny rychlosti s časem)

Přímočará síla (hmotnost krát zrychlení)

Přímočarý moment (hmotnost krát rychlost)

Kruhový pohyb má odpovídající veličiny:

Úhlové přemístění (úhel)

Úhlová rychlost (míra změny úhlu s časem)

Úhlové zrychlení (míra změny úhlové rychlosti s časem)

Úhlová síla (krouticí moment)

Úhlový moment (úhlová rychlost krát moment setrvačnosti)

Při zachování momentu jsme zřejmě nuceni zachovat přímočarý a úhlový moment odděleně. Jestliže se rotující objekt pohybuje po přímce, rotační moment nepřispívá ničím k přímočarému momentu a naopak.

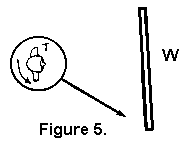
Podobně, jestliže osoba stojí na otočné plošině T, jak je zobrazeno na obr. 5, a udělá jednu otáčku za sekundu, je lhostejné, jestli plošina stojí nebo se pohybuje libovolnou rychlostí – osoba na plošině T uvidí zeď W jednou za sekundu.

A PŘESTO....

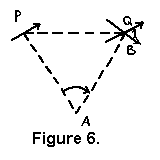
Jestliže se objekt, nakreslený na obr. 5 pohybuje po přímce, tohoto v podstatě přímočarého pohybu lze dosáhnout dvěma čistými rotacemi. Na obr. 6 se objekt pohybuje z bodu P do bodu Q a tohoto pohybu je dosaženo dvěma rotacemi, jednou kolem bodu A a druhou kolem bodu B.

PŘEMÍSTĚNÍ HMOTY KRUHOVÝM POHYBEM

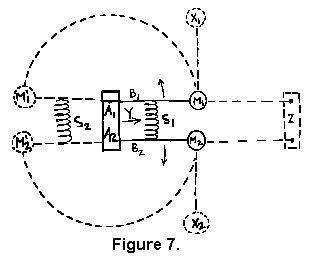
Je tedy možné pomocí kruhového pohybu přemístit hmotu? Soustava zobrazená na obr. 7 vypadá slibně. Hmotnosti M1 a M2 jsou zpočátku poháněny bočně pomocí stlačené pružiny S1. Potom rotují kolem středů A1 a A2, přičemž jsou omezeny pouze dvěma lehkými tyčemi B1 a B2. Dostanou se do bodů M1' a M2', kde je jejich kinetická energie absorbována druhou pružinou S2. Pohybuje se těžiště této soustavy v prostoru?

Opravdu ne! Po celou dobu hmoty rotující kolem středů A1 a A2 způsobují odstředivé síly a1 a a2. Prvních 90 stupňů rotace urychlují centrální blok s otočnými čepy A1 a A2 doprava ve směru šipky Y. Dalších 90 stupňů rotace zpomalují centrální blok až do klidu. Děje se pouze to (za předpokladu, že hmotnost centrálního bloku je nula), že hmotnosti M1 a M2 se budou pohybovat bokem do poloh X1 a X1 a potom se vrátí do své původní polohy. Centrální blok se mezitím bude pohybovat z původní polohy Y do polohy Z. Získá maximální rychlost v okamžiku, kdy obě hmotnosti jsou v polohách X1 a X2.

K žádnému přesunu hmoty nedojde. Dokonce ani tehdy, když samotný centrální blok má hmotnost, se těžiště soustavy nepohybuje.

PRŮLOM

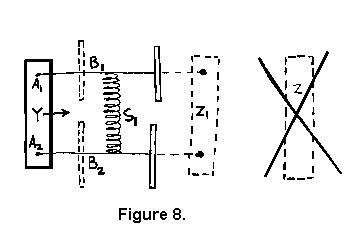
Objevili jsme, že když hmotnosti M1 a M2 nejsou „mrtvé“ hmoty, ale rotující kola (na obr. 8 zobrazeny z profilu), blok s čepy se nepohybuje z bodu Y do bodu Z, jako na obr. 7, ale o menší vzdálenost Z1. Tudíž, dokonce i v případě, že blok s čepy má hmotnost, výsledkem rotací hmotností M1 a M2 okolo středů A1 a A2 o 180 stupňů je, že těžiště se pohnulo doleva.

Experimenty skutečně prokázaly, že odstředivé síly vyžadované rotujícími koly, které vykonávají precesi tímto způsobem, jsou menší než hodnoty vypočítané z jednoduché mechaniky. Redukce odstředivé síly závisí na „kvalitě“ kol a způsobu precese. Kvalita kola závisí na relativní velikosti obruče a na jeho průměru a velikosti hmotnosti, která je na této obruči. Čím je tedy obruč užší a čím víc je na ni hmoty, tím „lepší“ kolo bude. Podobně, čím rychleji se kolo otáčí vzhledem k rychlosti precese a čím je větší poloměr rotujícího kola vzhledem k poloměru precese, tím menší bude odstředivá síla.

Abychom dosáhli působivého snížení odstředivé síly, potřebujeme velké těžké kolo s velmi tenkou obručí, běžící velmi rychle a konající precesi pomalu kolem malého poloměru.

Experimentálně bylo ověřeno, že - s kolem vysoké kvality, které koná precesní pohyb kolem poloměru, který je dvacetkrát menší než je poloměr kola, s rychlostí, která je stokrát vyšší než je rychlost precese - se odstředivá síla zmenšila proti vypočítanému předpokladu na méně než jednu desetinu..

VYUŽITÍ

K přesunu hmoty dochází bez vnější síly působící na soustavu. Rotující kola nekorespondují s přímočarými veličinami, včetně přímočaré síly. Při návratu hmoty do její původní polohy v prostoru mohou být použity jakékoli prostředky, které neodklánějí osu rotace. Takový zpětný pohyb produkuje reakční sílu, dokonce proti odporující síle. Jestliže je přítomna odporující síla, práce vykonaná proti tomuto odporu je dodávána mechanismem, ne kolem. V žádném čase během cesty obnovování nemá zařízení jako celek žádný přímočarý moment.

Jestliže je precesní pohyb zkombinován s konvenčním přímočarým pohybem cyklickým způsobem – a existuje mnoho způsobů, jak to udělat – je možné produkovat spojité sinusové přemisťování a tudíž, ve vícefázové verzi, nepřetržité, stálé přemisťování. V okamžiku, kdy se mechanismus zastaví, tak soustava nevykonává žádný pohyb. Mechanismus není více schopen produkovat kinetickou energii, jinou než je produkována momentem.

ALE, přemisťování hmoty, dokonce proti odporující síle, je pozitivně možné.

KROUTICÍ MOMENT A PRECESE

Experimenty se setrvačnými hmotami prováděné v pozemské laboratoři jsou náchylné podléhat gravitačním silám, které jsou velké v porovnání s těmi, které jsou měřeny.

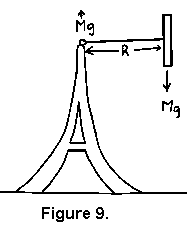
Gyroskopy-hračky, vyrobené proto, aby konaly precesní pohyb kolem modelu Eiffelovy věže, to dělají jako výsledek krouticího momentu MgR (viz obr. 9) odvozeného od hmotnosti gyroskpu, a uplatňují tah vzhůru na věž. Zkušenost s gyroskopy tohoto typu dává vzniknout myšlence, krouticí moment je zapříčiněn precesí.

Podobná myšlenka trvá v elektrotechnickém inženýrství, kdy napětí je příčinou elektrického proudu. Můžeme se s tím setkat u našich komerčních elektrických zařízení a u přístrojů v domácnosti, které jsou všechny spojeny paralelně ke zdroji elektrického napětí, kde proud odebíraný jednotlivými spotřebiči závisí na odporu tak, že I = e/R.

Kdybychom chtěli posílat pevně daný proud skrze všechny naše přístroje zapojené v sérii, napětí vyvinuté pro celý obvod by bylo dáno vztahem e = iR a bylo by spíš viděno jako výsledek proudu než jeho příčina.

Stejným způsobem může být gyroskop přinucen konat precesní pohyb po určené dráze. Jestliže krouticímu momentu takto generovanému brání soustava (nebo dokonce jiný gyroskop) a tento je měřen, zjistí se, že gyroskop bude vyžadovat právě takový krouticí moment, potřebný pro precesi a že precese je v tomto případě příčinou krouticího momentu.

UMÍSTĚNÍ OSY

Gyroskop, který je ve skutečnosti pouze setrvačník, je v podstatě třírozměrné zařízení. Stejně jako směr rotace elektrického motoru může být určen ze směru magnetického pole a elektrického proudu tím, že budeme držet dva prsty a palec vzájemně v pravém úhlu podle známého Flemingova zákona levé ruky, tak směr rotace, momentu a krouticího momentu může být použit k předpovězení směru precese.

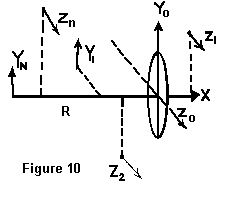
Jestliže točivý moment kola je ve směru X, (viz obr. 10), potom krouticí moment kolem osy Y, v pravém úhlu k rovině nákresu, bude vykonávat precesní pohyb kolem osy Z, kolmo na rovinu nákresu.

Je zajímavé, že se gyroskop jeví jako lhostejný k přesnému umístění osy ve směru Y, které může být v Y1 nebo Y2, atd... až Yn, pokud jsou rovnoběžné. Podobně výsledná precese může probíhat kolem osy Z nebo Z1, Z2 ... Zn. Žádná konkrétní osa ve směru Y nemá vztah k žádné konkrétní ose ve směru Z.

Následující rovnice je univerzální.

Krouticí moment (kolem jakékoli osy v rovině Y) = úhlový moment (gyroskopu) x precesní úhlová rychlost (kolem jakékoli osy v rovině Z)

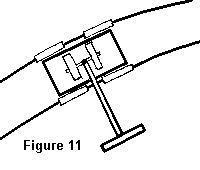
Takže vlak-hračka na spojitě zakřivené dráze, jak je zobrazeno na obrázku 11, je poháněn po trati a dokonce do kopce pomocí ramene nesoucí rotující kolo W, které je otočně uloženo tak, aby mohlo volně vertikálně padat vlivem tíže, ale přenáší svůj krouticí moment horizontálně podvozku. Do určité míry je nezávislý na poloměru trati, jak nám bylo poprvé předvedeno v roce 1975.

Přesně tato vlastnost umožňuje přemisťování hmoty, jak je nakresleno na obr. 6, jako výsledek dvou jednoduchých rotací kolem rovnoběžných os skrze A a B. Základní rozdíl mezi precesí kolem osy Yo, která prochází těžištěm rotujícího kola a precesí kolem každé jiné osy Yn je ten, že kolu je udělena příslušná velikost lineárního momentu Mv ve směru Z tak, že tato tečná precesní rychlost v bude rovna vzdálenosti R krát úhlová rychlost. Je to tento přímočarý moment, který je způsoben úhlovým momentem a který umožňuje dosažení přemístění hmoty.

E.R. Laithwaite
W.R.C. Dawson
September 1994

Pictures reduced in size, touched up, and coded into this document
by David E. Cowlishaw, 24 March 1998, for inertial propulsion researchers.
Gyroscopic Inertial Thruster Page

Back to main page

Z angličtiny přeložil Ladislav Kopecký